QAQ

1. $R$ 表示外接圆半径， $r$ 表示内接圆半径.

正弦定理

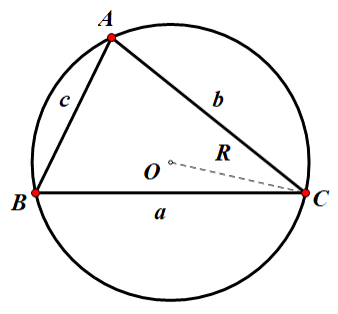
如图，对于任意 $\triangle \rm ABC$ ，有 $$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R$$

余弦定理

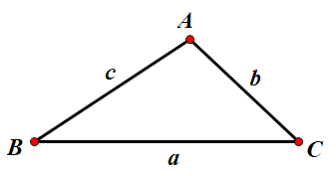
如图，对于任意 $\triangle \rm ABC$ 中有 $$a^2 = b^2 + c^2 - 2bc\cos A \\\ b^2 = a^2 + c^2 - 2ac\cos B \\\ c^2 = a^2 + b^2 - 2ab\cos C \\\ \cos A = \frac{b^2 + c^2 - a^2}{2bc} \\\ \cos B = \frac{a^2 + c^2 - b^2}{2ac} \\\ \cos C = \frac{a^2 + b^2 - c^2}{2ab}$$

三角形内接圆与三边的关系

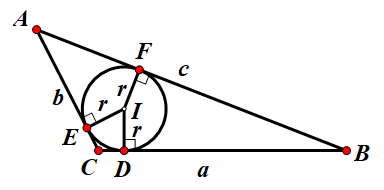
如图，对于任意 $\triangle \rm ABC$ ，其内切圆半径 $$r = \frac{ab\sin C}{a + b + c}$$

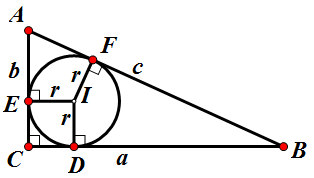
特殊地，当 $\triangle \rm ABC$ 为直角三角形时，其内切圆半径还可表示为 $$r = \frac{a + b - c}{2}$$

中线长定理

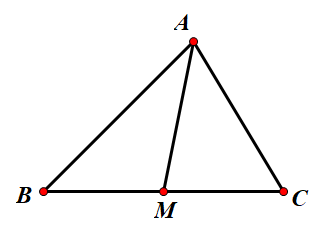
如图，对于任意 $\triangle \rm ABC$ ， $M$ 点是 $BC$ 边的中点，则有 $$AB^2 + AC^2 = 2BM^2 + 2AM^2$$

倍角公式

$$\sin 2 \alpha = 2\sin \alpha \cos \alpha \\\ \cos 2 \alpha = 2 \cos ^2 \alpha - 1 \\\ \tan 2\alpha = \frac{2\tan \alpha}{1 - \tan ^2 \alpha}$$

和差角公式

$$\sin(\alpha + \beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha \\\ \cos(\alpha + \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \\\ \tan(\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} \\\ \\\ \sin(\alpha - \beta) = \sin \alpha \cos \beta - \sin \beta \cos \alpha \\\ \cos(\alpha - \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \\\ \tan(\alpha - \beta) = \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta}$$

三倍角公式

$$\sin 3 \alpha = 3 \sin \alpha - 4 \sin^3 \alpha \\\ \cos 3 \alpha = -3 \cos \alpha + 4 \cos^3 \alpha$$

梅涅劳斯定理

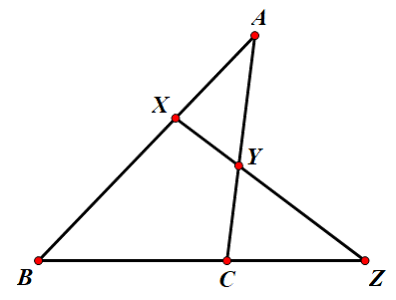
如图，对于任意 $\triangle \rm ABC$ 被直线 $XYZ$ 所截，有 $$\frac{AX \cdot BZ \cdot CY}{XB \cdot ZC \cdot YA} = 1$$ .

逆定理：

如图，若三角形被 $X$ 、 $Y$ 、 $Z$ 三点所连的线段所截，如果满足 $$\frac{AX \cdot BZ \cdot CY}{XB \cdot ZC \cdot YA} = 1$$ 则可说明 $X$ 、 $Y$ 、 $Z$ 三点共线.

塞瓦定理

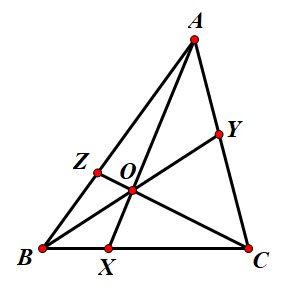
如图，对于任意 $\triangle \rm ABC$ 中任取一点 $O$ ，延长 $AO$ 、 $BO$ 、 $CO$ 分别交对边于 $X$ 、 $Y$ 、 $Z$ ，则有 $$\frac{AZ \cdot BX \cdot CY}{ZB \cdot XC \cdot YA} = 1$$ .

逆定理：

如图，若三角形内一点与三边上任意一点连线若满足 $$\frac{AZ \cdot BX \cdot CY}{ZB \cdot XC \cdot YA} = 1$$ 则可说明 $AX$ 、 $BY$ 、 $CZ$ 三线共点.

斯特瓦尔特定理

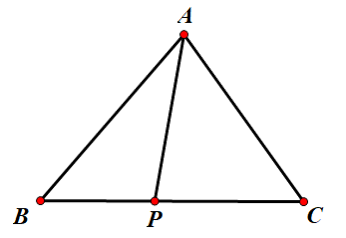
如图，对于任意 $\triangle \rm ABC$ 中在任意一边上任取一点 $P$ ，存在 $$AB^2 \times PC + AC ^2 \times BP - AP^2 \times BC = BC \times PC \times BP$$

相交弦定理

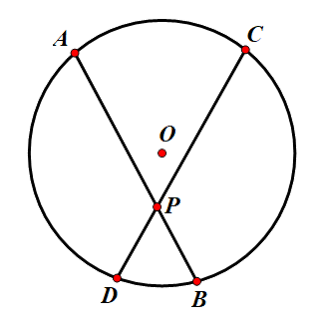
如图，对于圆内任意两条不平行的弦 $AB$ 与 $CD$ 相交于点 $P$ ，存在 $$PA \times PB = PC \times PD$$

切割线定理

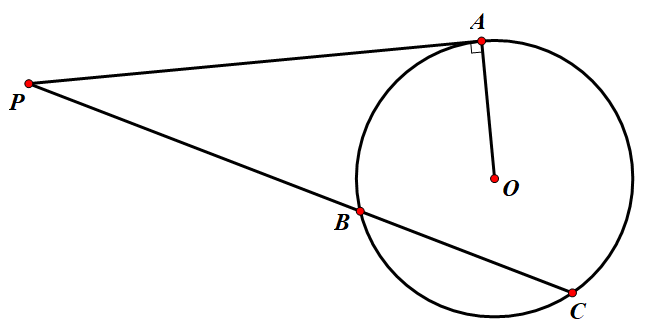
如图，对于平面内一点 $P$ 做引圆的切线 $PA$ 与割线 $PBC$ ，存在 $$PA^2 = PB \times PC$$

割线定理

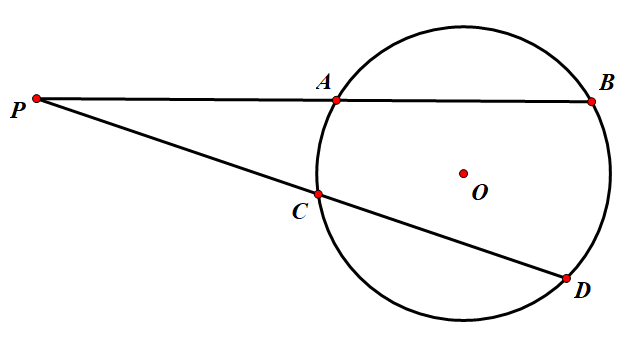
如图，对于平面内一点 $P$ 做引圆的两条割线 $PAB$ 与 $PCD$ ，存在 $$PA \times PB = PC \times PD$$

射影定理

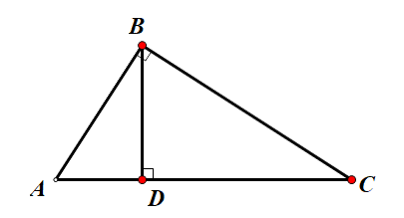
如图，在 $Rt \triangle ABC$ 中， $BD$ 为 $AC$ 边上的垂线，存在 $$BD^2 = AD \times CD$$

托勒密定理

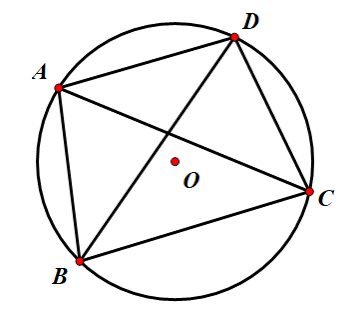
如图，圆内接四边形 $ABCD$ ，存在 $$AB \times CD + AD \times BC = AC \times BD$$

常用（必备）不等式

基本不等式

$$\frac{2}{\frac{1}{a_1} + \frac{1}{a_2}} \le \sqrt{a_1 a_2} \le \frac{a_1 + a_2}{2} \le \sqrt{\frac{a_1^2 + a_2^2}{2}}$$

广义：

$$\frac{n}{\sum_{i=1}^{n} \frac{1}{a_{i}}} \le \sqrt[n]{a_{1} a_{2} \cdots a_{n}} \le \frac{\sum_{i=1}^{n} a_{i}}{n} \le \sqrt{\frac{\sum_{i=1}^{n} a_{i}^{2}}{n}} (\text{取等条件：}a_1 = a_2 = a_3 = \cdots = a_n)$$

柯西（Cauchy）不等式

$$\left(\sum_{i=1}^{n} a_{i}^{2}\right) \times\left(\sum_{i=1}^{n} b_{i}^{2}\right) \geq \left(\sum_{i=1}^{n} a_{i} b_{i}\right)^{2}$$

辅助角公式

$$a \sin \alpha \pm b \cos \alpha=\sqrt{a^{2}+b^{2}} \sin (\alpha \pm \varphi)$$

点到直线距离

对于直线方程为 $Ax + By + C = 0$ ，点 $P$ 的坐标为 $(x_0, y_0)$ ，则点 $P$ 到直线的距离为 $$d = \left|\frac{A x_0+B y_0+C}{\sqrt{A^2+B^2}}\right|$$